Karnaugh Map Solver
Simplify Boolean logic with step-by-step K-Map solutions
What is Karnaugh Map Solver? Complete Overview
The Karnaugh Map Solver is a free online tool designed to simplify Boolean logic expressions effortlessly. It supports five different input methods: Karnaugh Map, Truth Table, Boolean Expression, Minterm, or Maxterm numbers - all with don't-care condition support. This tool is particularly valuable for students, engineers, and professionals working with digital logic design, helping them visualize and simplify complex Boolean expressions. The solver provides detailed step-by-step simplification processes, shows original and simplified expressions, visual grouping maps, and even auto-generates circuit diagrams. With its intuitive interface and comprehensive output options, it significantly reduces the time and effort required for manual K-Map simplification while minimizing errors.
Karnaugh Map Solver Interface & Screenshots
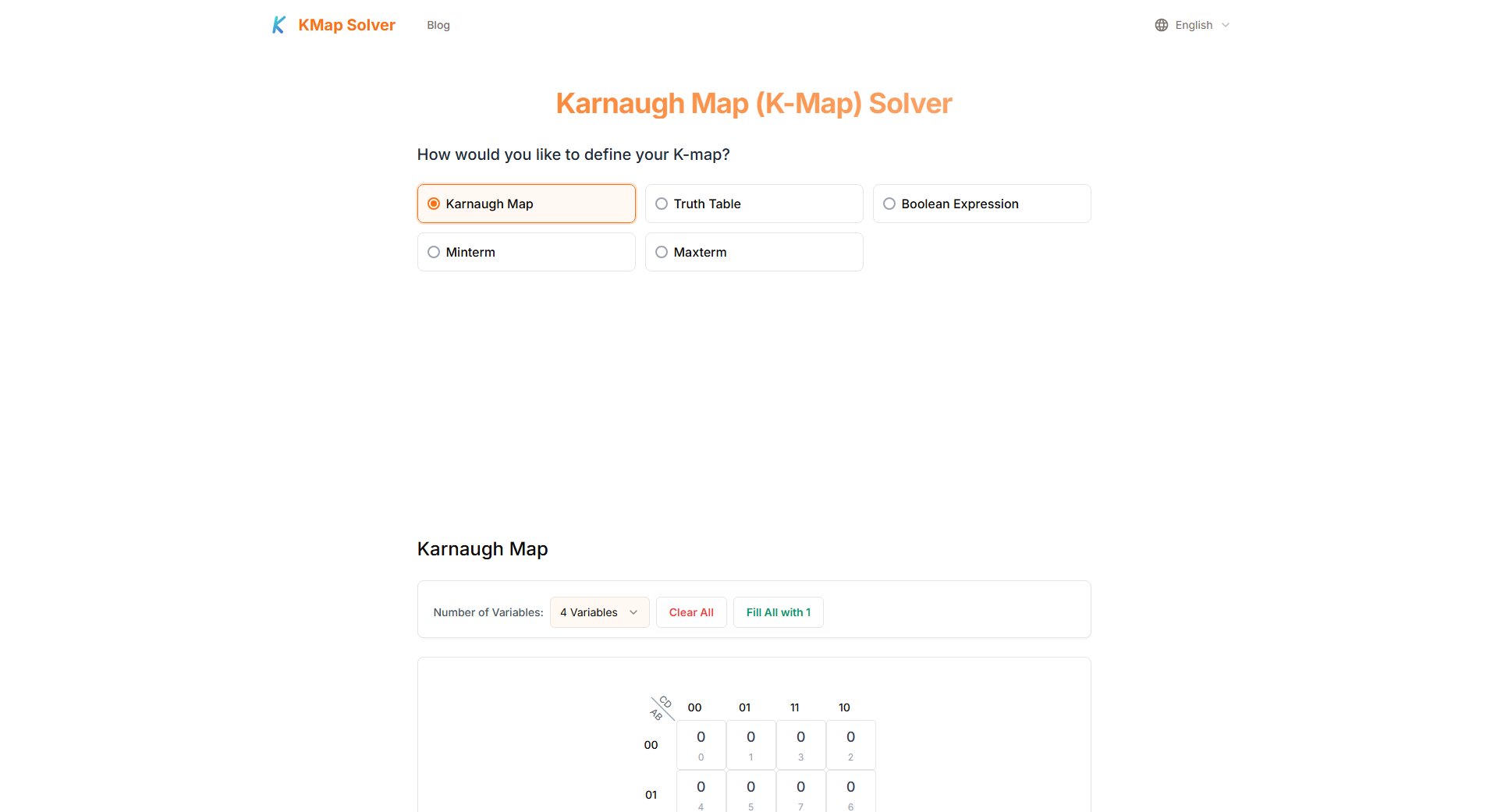
Karnaugh Map Solver Official screenshot of the tool interface
What Can Karnaugh Map Solver Do? Key Features
Multiple Input Methods
The solver offers five flexible input options: Karnaugh Map, Truth Table, Boolean Expression, Minterm, or Maxterm numbers. This versatility allows users to start from whichever representation they're most comfortable with or have available. The tool uniquely supports don't-care conditions (represented by X) in all input methods, providing complete flexibility for real-world digital design scenarios where certain input combinations may be irrelevant.
Flexible Output Formats
Users can choose between Sum of Products (SOP) and Product of Sums (POS) output formats based on their requirements. The tool automatically generates both the original and simplified Boolean expressions, allowing for easy comparison. This feature is particularly useful when optimizing digital circuits for different design constraints or when specific output forms are required for implementation.
Step-by-Step Visualization
The solver provides a detailed, visual breakdown of the simplification process. Users can see exactly how terms are grouped in the K-Map, with color-coded visualizations that make the grouping logic clear. This educational aspect helps users understand the underlying principles of K-Map simplification, making it an excellent learning tool alongside being a practical solver.
Circuit Visualization
A unique feature of this solver is its ability to automatically generate circuit diagrams corresponding to the simplified Boolean expressions. These visual representations show both the gate-level implementation and the logic flow, helping users translate abstract expressions into practical circuit designs. The diagrams update in real-time as inputs change.
Solution PDF Download
Users can download comprehensive PDF reports of their solutions, including the input data, all intermediate steps, final simplified expressions, and circuit diagrams. This feature is particularly valuable for students needing to submit assignments or professionals documenting their design processes.
Best Karnaugh Map Solver Use Cases & Applications
Digital Logic Design Homework
Electrical engineering students can use the solver to verify their manual K-Map solutions for class assignments. The step-by-step visualization helps them understand where they might have made grouping errors, while the PDF download feature creates professional-looking submissions.
FPGA Programming Preparation
Hardware designers working with FPGAs can quickly simplify complex Boolean expressions before implementation. The circuit visualization helps bridge the gap between abstract logic and hardware description languages like VHDL or Verilog.
Industrial Control System Optimization
Control system engineers can simplify logic for PLC programming by inputting their truth tables and obtaining optimized Boolean expressions. The don't-care condition support is particularly valuable for real-world systems with undefined states.
Computer Architecture Education
Professors can use the tool during lectures to demonstrate K-Map principles interactively. The real-time visualization helps students grasp the concepts of logical adjacency and optimal grouping more effectively than static textbook examples.
How to Use Karnaugh Map Solver: Step-by-Step Guide
Select your preferred input method from the five available options: Karnaugh Map (interactive grid), Truth Table (input/output values), Boolean Expression (algebraic form), Minterm numbers, or Maxterm numbers. The interface adapts dynamically to your choice, showing the appropriate input fields.
Enter your logic function values. For K-Map input, simply click cells to toggle between 0, 1, and X (don't care). For truth tables, fill in the output column. Expression input accepts standard Boolean notation. Minterm/Maxterm inputs accept comma-separated numbers. Use the 'Fill All with 1' or 'Clear All' buttons for quick setup.
Choose your desired output format (SOP or POS) using the toggle switch. The tool will immediately process your input and display preliminary results. You can switch between formats at any time to see alternative simplifications.
Explore the detailed solution breakdown. The interface shows the original expression, simplified expression, grouped K-Map cells (with color coding), and the logical grouping rationale. Hover over elements to see detailed explanations of each simplification step.
View the automatically generated circuit diagram that implements your simplified expression. The diagram shows both the gate-level implementation and signal flow. Use the zoom and pan controls to examine details.
Validate your results using the auto-generated truth table that verifies the equivalence between original and simplified expressions. When satisfied, download the complete solution as a PDF report for offline reference.
Karnaugh Map Solver Pros and Cons: Honest Review
Pros
Considerations
Is Karnaugh Map Solver Worth It? FAQ & Reviews
Don't care conditions (represented by X) are input combinations where the output value doesn't matter in the actual application. The solver can treat these as either 0 or 1 to achieve the most optimal simplification. This is particularly useful in real-world digital design where certain input states never occur or where the output in those states is irrelevant.
SOP (Sum of Products) represents the function as ORed combinations of AND terms, while POS (Product of Sums) represents it as ANDed combinations of OR terms. The solver shows both forms so you can choose which better suits your implementation needs. SOP often results in simpler AND-OR implementations, while POS may be better for NOR-only implementations.
Simply toggle the output format selector to 'POS' after entering your input. The solver will automatically regroup the K-Map zeros (instead of ones) and generate the Product of Sums form. All visualizations and circuit diagrams will update to show the POS implementation.
Select 'Maxterm' as your input method and enter the Maxterm numbers (comma-separated) corresponding to the output 0's in your truth table. For example, if your function outputs 0 for input combinations 0, 2, and 5, you would enter '0,2,5'. The solver will automatically generate the complete truth table and K-Map from these.
Currently, the solver supports up to 4-variable K-Maps (16 cells) which covers the majority of educational and practical applications. Five-variable K-Maps would require a three-dimensional representation that's less practical for online implementation while providing diminishing returns in simplification benefits.